Hi Everyone, Welcome To CBSE Digital Education. Today We Are Going To Discuss an interesting Topic About the definition of circular motion. CBSE Digital Education provides all important information regarding the definition of circular motion. Read this complete article till the end.
Definition of Circular Motion
When an object moves in a circle is known as circular motion. The motion of a body can be linear or circular. However, they differ in a number of ways as listed in the table given below:
| Linear Motion | Rotational Motion |
| Displacement = x | Angular displacement = θ |
| Velocity = dx/dt | Angular velocity, = d /dt |
| Mass M | Moment of Inertia I |
| Force = Ma | Torque, = Ix |
| Power = Fv | Power, p = τω |
| Acceleration = a = dv/dt | Angular displacement, = d /dt |
| Work = Fds | Work = τdθ |
| Kinetic energy, k = ½ mv2 | Kinetic energy, k = ½ Iω 2 |
| Linear momentum, p = m x v | Angular momentum, L = I x ω |
Types of Circular Motion:
What is the Uniform Circular Motion?
It describes the motion of a body traversing a circular path at a constant speed. When the body describes circular motion, its distance from the axis of rotation remains constant at all times. Though the body’s speed is constant its velocity is not constant, velocity being vector quantity depends on both the speed of the body and its direction of travel. This changing velocity indicates the presence of accelerated motion.
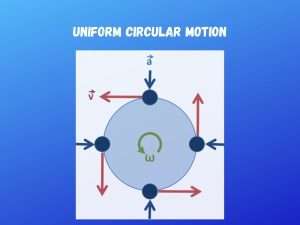
The centripetal acceleration of constant magnitude is directed at all times toward the axis of rotation. This acceleration is, in turn, produced by the centripetal force which is also constant in magnitude and directed towards the axis of rotation.
In the case of rotation around a fixed axis of a rigid body that is not negligibly small compared to the radius to the path, each particle of the body describes a uniform circular motion with the same angular velocity, but with velocity and acceleration are different with the position concerning the axis.
Example of Uniform Circular motion
- An artificial satellite moves in a uniform circular motion around the Earth.
- The earth moves around the sun in a uniform circular motion.
- Cyclists moving on a circular path with a constant speed exhibit uniform circular motion.
Formula related to uniform circular motion
For motion in a circle of radius r, the circumference of the circle, C = 2 r. If the time for one rotation is T, the angular rate of rotation is also called angular velocity and the unit is radian/second.
ω = 2π /T = πf = θ/T
The speed of the body traveling the circle is:
V = 2π r/T = ωr
The angle swept out in a time t is given below
θ = 2 πf = ωt
The angular acceleration, of the particle, is given below
α = dω /dt
In the case of uniform circular motion, will be zero. The acceleration due to the change in the direction is given below
α = v2/r = ω 2r
The centripetal and centrifugal force can also be searched out using acceleration
Fc = ma = mv2/r
Consider a body of 1 kilogram, moving in a circle of radius 1 meter, with an angular velocity of 1 radian per second, then
- The speed is 1 meter per second.
- Inward acceleration is 1 meter per square second, v2/r.
- The momentum of the body is 1kg.m.s-1.
- The moment of inertia is 1kg.m2.
- It is subject to a centripetal force is one meter per square second, which is 1Newton.
- The period of the circular motion is 2π seconds per turn.
- The angular momentum is 1kg.m2.s-1.
- Kinetic energy is ½ joule.
- The circumference of the orbit is 2π meters.
- The frequency is (2π )-1 or 1/2π hertz (Hz).
What is Non-uniform Circular Motion?
An object moving in a circular path with a varying speed is considered to be in a non-uniform circular motion. If the speed is changing, there is tangential acceleration in addition to normal acceleration.
In a non-uniform circular motion, the net acceleration (a) is along the direction of Δv which is directed inside the circle but does not pass through its center as shown in the figure. The net acceleration may be resolved into two components: tangential acceleration and normal acceleration, also known as the centripetal or acceleration, also known as the centripetal or radial acceleration. Different tangential acceleration and centripetal acceleration are present in both uniform and non-uniform circular motion.
In a non-uniform circular motion, normal force does not always mark in the opposite direction of weight. With a uniform circular motion, the only force acting upon a body traveling in a circle is the centripetal force.
In a non-uniform circular motion, additional forces are acting on the body due to a non-zero tangential acceleration. Although additional forces are acting upon the object, the sum of all the forces acting on the object will have to be equal to the centripetal force.
What is the Centripetal Force?
For a particle to move in a circular motion, it must be acted upon by a net force towards the center. This force is called the Centripetal force.
The centripetal force, Fc = mac = mv2/r
Fc = mω 2r = mv2/r
ac = ω2r = v2/r
This acceleration is known as Centripetal Acceleration.
What is Centrifugal force?
Circular motion is an accelerated motion. If we observe the motion of any particles w.r.t an accelerated frame, it is acted upon by a pseudo force.
- If a particle is observed from a frame in a circular motion, it is acted by a pseudo force, called a centrifugal force.
- The pseudo force acts in the direction opposite to the acceleration of the frame.
Difference between Centripetal and Centrifugal force
- The centrifugal force is the tendency of an object to fly away from the center of curvature being the inertia of motion but the centripetal force is the force that keeps an object moving with uniform speed along a circular path.
- Centrifugal force acts along the radius of the circle from the center towards the object but centripetal force acts as the radius of the circle from the object towards the center.
- Centrifugal force is directed along the radius from the center towards the object such as the mud flying o
- ff a tire or children being pushed outward on a revolving roundabout but the centripetal force is directed towards the center of the circle such as a satellite orbiting Earth or a planet.
We hope you like this article about the Inviting applications for the definition of circular motion If you want to ask any queries regarding the definition of circular motion then message us in the comment section, and we will reply to you soon.
Click here for More CBSE News